Let’s say you have a list, and you want to “interleave” or “riffle shuffle” the items in it. That is, you want to split the list in two, and then make a new list, alternating items from the first and second halves. In Python, there are a number of ways of doing this. Now we are left with the problem of which of these ways should we actually implement? One key factor in making this decision is performance: how well do the various methods actually perform. I decided to run a little experiment.

Step one: refactoring

I took most of the solutions from the above list and rewrote them so they all use a similar vocabulary, to make them easier to compare. Why only most? Well, some solutions are pretty similar so I didn’t include near duplicates. Here are the solutions, as rewritten by me. Each solution is named for the stackoverflow username who posted the solution.

First up is ernesto’s solution. This is a pretty straightforward loop, adding two elements to a new list on each pass. We then have to check whether there’s an additional element to add at the end (i.e. if the original list had an odd number of elements).

def interleave_ernesto(lst):
    half_len = len(lst)//2
    lst_one, lst_two = lst[:half_len],lst[half_len:]
    lst_output = []
    num = 0
    while num< half_len:
        if len(lst_one)>=num:
            lst_output.append(lst_one[num])
            lst_output.append(lst_two[num])
        num += 1
    if len(lst)%2 != 0:
        lst_output.append(lst_two[num])
    return lst_output

Next we have Oscar’s suggestion, which is a neat recursive solution. This is actually Ernesto’s modification of the original suggestion.

def interleave_oscar(lst):
    def interleaveHelper(lst_one,lst_two):
        if not lst_one:
            return lst_two
        elif not lst_two:
            return lst_one
        return lst_one[0:1] + interleaveHelper(lst_two, lst_one[1:])
    return interleaveHelper(lst[:len(lst)//2], lst[len(lst)//2:])

Another approach starts by splitting the list in two, and then directly modifying one of those halves (rather than creating a third list lst_output as above). This involves figuring out what index to add the additional elements in at.

def interleave_russia(lst):
    half_len = len(lst) // 2 
    lst_one, lst_two = lst[:half_len], lst[half_len:]
    for index, item in enumerate(lst_two):
        insert_index = index*2 + 1
        lst_one.insert(insert_index, item)
    return lst_one

Alternatively, we could take our two half-lists and zip them into a list of pairs, and then extend a new list by each pair. Again this involves a check for odd lists at the end.

def interleave_raiyan(lst):
    half_len = len(lst)//2
    lst_one,lst_two = lst[:half_len], lst[half_len:]
    lst_zip = zip(lst_one,lst_two)
    lst_output = []
    for pair in lst_zip:
        lst_output.extend(list(pair))
    if len(lst)%2==1:
        lst_output.append(lst_two[half_len])
    return lst_output

Yet another approch is to turn each half-list into an iterator, and then make use of next to take the next element of each iterator at each stage.

def interleave_audionautics(lst):
    half_len =len(lst)//2
    iter_one,iter_two = iter(lst[:half_len]), iter(lst[half_len:])
    lst_output = []
    for i in range(half_len):
        lst_output.append(next(iter_one))
        lst_output.append(next(iter_two))
    lst_output += list(iter_two)
    return lst_output

Konstyantyn proposed two solutions, neither of which worked for odd-numbered lists as written on the SO page (the middle element is added at the end, rather than the last element). So I fixed them. There may be a more elegant way to fix the problem. This solution works by simply calculating the index at which the next element of the shuffled list is in the original list. The trick is that +(i%2)\*half_len either does nothing (if i is even) or shifts you to the middle of the list (if i is odd).

def interleave_konstyantyn_one(lst):
    lst_output = []
    half_len = len(lst) // 2
    for i in range(len(lst)):
        lst_output.append(lst[i // 2 + (i % 2) * half_len])
    return lst_output[:-1] + lst[-1:]

And konstyantyn’s second solution (again, modified to work on odd-numbered lists) is basically the same idea but more explicit using an if/then construction.

def interleave_konstyantyn_two(lst):
    lst_output=[]
    half_len = len(lst)//2
    for i in range(len(lst)):
        if not i%2:
            lst_output.append(lst[i//2])
        else:
            lst_output.append(lst[i//2 + half_len])
    return lst_output[:-1] +lst[-1:]

Next we have the solution that took me the most time to figure out. It’s relying on a couple of interesting features of python. First, sum is a built in function which is not just “sum numbers” but basically “reduce, but only if the operation is +”. That’s what the optional second argument of sum is: the initial value for your summing. And since you can concatenate lists (or tuples) with +, this works with list structures. What about the additional + tuple(iter_two)? The neat thing about iterators is that their elements are consumed when they’re used. What this means is that if the original list had an even number of elements, then zip would have consumed all of iter_two, and so tuple(iter_two) will be empty. However, if the original list had an odd number of elements, then zip would have consumed all but one element of iter_two, and so tuple(iter_two) will be simply the final element of the list that needs appending to complete the shuffle. Very neat.

def interleave_paul(lst):
    half_len = len(lst)//2
    iter_one,iter_two = iter(lst[:half_len]),iter(lst[half_len:])
    return list(sum(zip(iter_one,iter_two), ())+ tuple(iter_two))

And finally, here’s a one-liner, because of course there is. This, again, needed fixing to accommodate odd-numbered lists. It’s basically Konstyantyn’s first solution boiled down to a list comprehension.

def interleave_shark(lst):
    return [lst[i//2 +i%2*(len(lst)//2)] for i in range(len(lst))][:-1] + lst[-1:]

Step two: checking they all work

OK so do all these snippets actually do what they’re supposed to? We know that the answer originally was “no” but the fixed up versions you see above all do pass this very simple test:

ODD_LIST  = [1,2,3,4,5,6,7]
EVEN_LIST = [1,2,3,4,5,6,7,8]
ODD_INTERLEAVED  = [1, 4, 2, 5, 3, 6, 7]
EVEN_INTERLEAVED = [1, 5, 2, 6, 3, 7, 4, 8]

def check_validity(func):
    pass_fail = "PASS" if func(ODD_LIST) == ODD_INTERLEAVED and func(EVEN_LIST) == EVEN_INTERLEAVED else "FAIL"
    print(f"{pass_fail}: {func.__name__}")

func_list = [
        interleave_russia,
        interleave_raiyan,
        interleave_audionautics,
        interleave_paul,
        interleave_ernesto,
        interleave_oscar,
        interleave_konstyantyn_one,
        interleave_konstyantyn_two,
        interleave_shark,
]

for func in func_list:
    check_validity(func)

I am here using the fact that you can get a string representation of the name of a python function func by using func.__name__.

Step three: performance

So they all work, but do they all work as well as each other? Let’s test how long each function takes to perform the shuffle on lists of varying sizes.

def size_check(f_list, n_list):
    size_dict={}
    for func in f_list:
        func_name = func.__name__
        size_dict[func_name] = {}
        func_dict= size_dict[func_name]
        for num in n_list:
            print(f"Trying {func_name} on list size {num}.")
            try:
                exec_string = f"{func_name}(list(range({num})))"
                t = timeit.Timer(stmt=exec_string,globals=globals()).autorange()
                func_dict[num] = t[1]*1e6 / t[0]
                print(f"{func_dict[num]} microseconds per loop.")
            except RecursionError:
                print("Recursion error, skipping.")
    return size_dict

Here’s what this function does. For each shuffle algorithm in f_list, it generates a dictionary where the key is the size of the list and the value is the time in microseconds to perform that operation. It does this for each list sized listed in n_list. These dictionaries are collected as the values in a big dictionary where the keys are the names of the shuffle algorithms. We can then import this dictionary into a pandas.DataFrame object.

Note here that we have to catch recursion errors, because we’ll bump into the recursion depth limit with our recursive solution. Why not increase the depth limit? We’ll see why I didn’t bother exploring that option in the next section.

Step four: graphing the output

OK, let’s take the data we get from our dictionary and plot list size against time. For the record, here’s the experiment I ran:

size_check(func_list, [5,10,20,50,100,200,500,1000,2000,5000,10000])

And here’s what that looks like when you graph it (on a log-log scale):

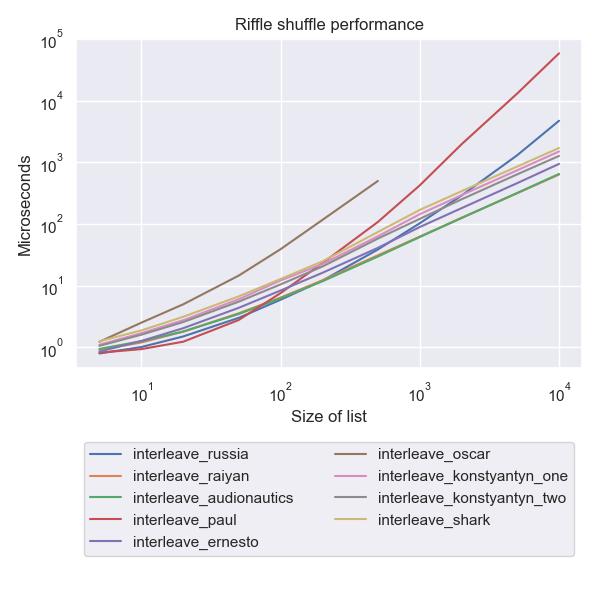
What we see here is that paul and russia appear to do well for small list sizes, but dramatically worse later on. audionautics appears to do pretty well for small sizes, and continues to do well for larger sizes. It’s hard to see from the graph here, but raiyan does pretty much exactly as well as audionautics. Note that the recursive solution is a lot slower even before it hits the recursion depth limit, which is why I didn’t explore raising the limit.

So let’s pick these four best performing algorithms, and explore more carefully how they perform at smaller sizes:

restricted_f_list = [
    interleave_russia,
    interleave_raiyan,
    interleave_audionautics,
    interleave_paul,
]
xpt2 = size_check(restricted_f_list,list(range(5,500,5)))

I ran the experiment out to 500, but I’m truncating it here. Note these are linear axes now.

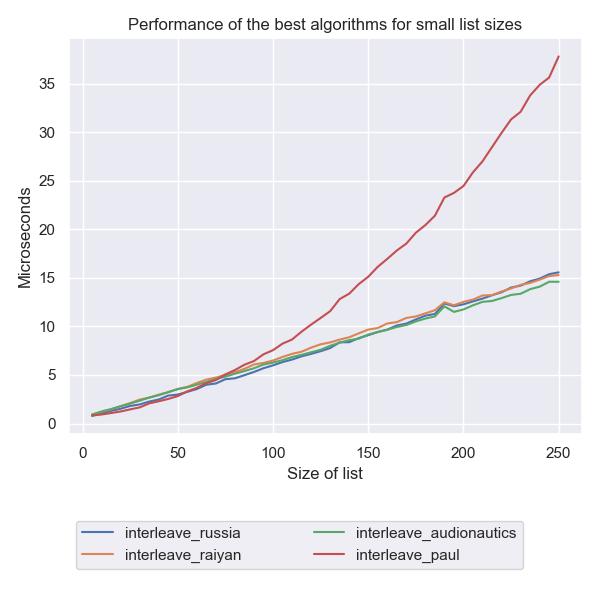
As is clear from this graphic paul doesn’t give you much advantage over the other well-performing solutions for small sizes, and it quickly becomes much worse. For these sizes, russia is essentially comparable. What’s also neat about this experiment is that we’re now fine-grained enough that we can see noise in the data: actual algorithm performance on my 7 year old desktop is a little variable.

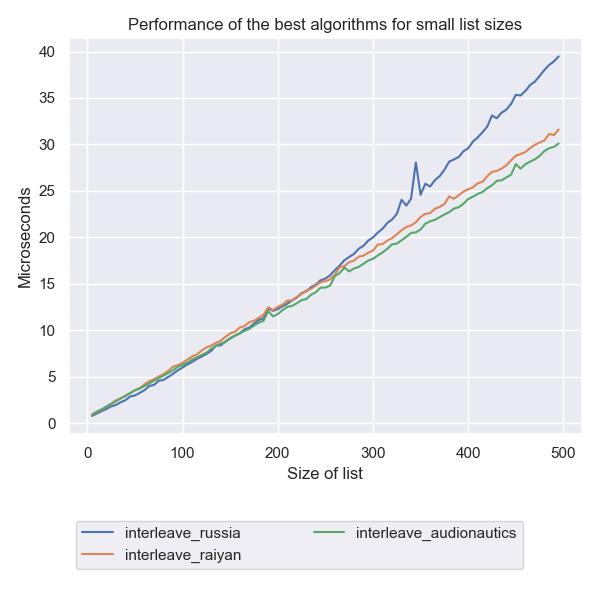
Finally, if we drop paul and zoom out to size 500, we see that russia starts to perform worse than the others at about 300. There is very little to choose between raiyan and audionautics. We can see even more noise in the data here. I don’t know what went on there! I could have repeated the timeit experiment several times and taken the minimum value, to limit the effect of this noise, but these experiments are quite slow already, and I think we can still see the trends pretty well even with this noise.

Conclusion

So, while I like the recursive solution (oscar), and paul’s clever sum trick, neither is advisable for a system where you value efficiency. Among the other solutions, the best performing ones are raiyan and audionautics. I have a slight preference for audionautics, since I find working with next quite a tidy approach.

License

The algorithm code snippets are all modified from answers on Stack Overflow and are released under the CC-BY-SA 3.0 license apart from interleave_shark and both interleave_konstyantyn snippets, which are CC-BY-SA 4.0.